حل نظام المعادلات في Microsoft Excel

يمكن أن تستفيد القدرة على حل أنظمة المعادلات في كثير من الأحيان ليس فقط في التعلم ، ولكن أيضًا من الناحية العملية. في نفس الوقت ، لا يعرف كل مستخدم للكمبيوتر الشخصي وجود متغيرات خاصة لحل المعادلات الخطية في Excel. دعونا معرفة كيفية تنفيذ هذه المهمة باستخدام أدوات مختلفة من هذا المعالج الجدول بطرق مختلفة.

خيارات للحلول

يمكن اعتبار أي معادلة حلها فقط عندما يتم العثور على جذوره. في Excel ، هناك العديد من الخيارات للعثور على الجذور. دعونا ننظر في كل واحد منهم.

الطريقة 1: طريقة Matrix

الطريقة الأكثر شيوعا لحل نظام المعادلات الخطية باستخدام أدوات Excel هي استخدام طريقة المصفوفة. وهو يتكون في بناء مصفوفة لمعاملات التعبيرات ، ثم في إنشاء مصفوفة عكسية. لنحاول استخدام هذه الطريقة لحل نظام المعادلات التالي:


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


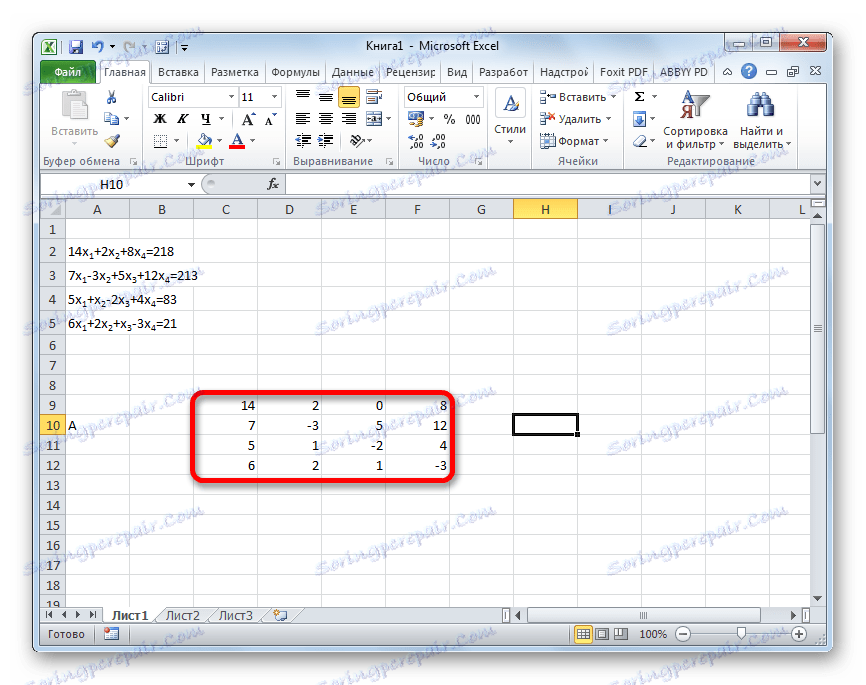
1. نملأ المصفوفة بأرقام معاملات المعادلة. يجب ترتيب هذه الأرقام بالتتابع بالترتيب ، مع مراعاة موقع كل جذر تتوافق معه. إذا كان أحد الجذور في أحد التعبيرات مفقودًا ، ففي هذه الحالة يعتبر المعامل مساويًا لصفر. إذا لم يتم الإشارة إلى المعامل في المعادلة ، لكن الجذر المطابق موجود ، يفترض أن يكون المعامل 1 . نحن نشير إلى الجدول الناتج باعتباره المتجه أ.
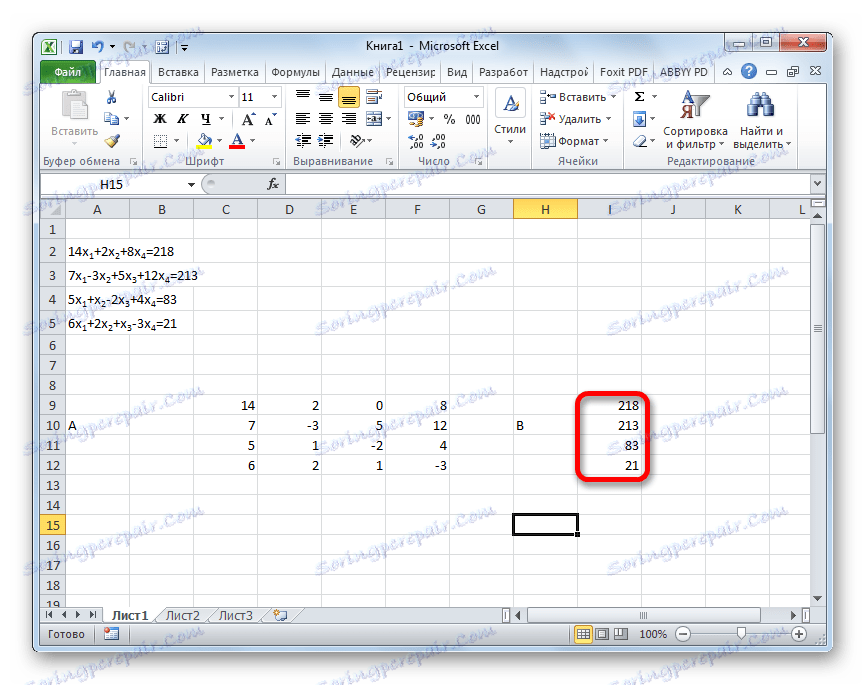
2. كتابة القيم بشكل منفصل بعد علامة "يساوي". حددهم باسمهم الشائع ، كالمتجه ب.
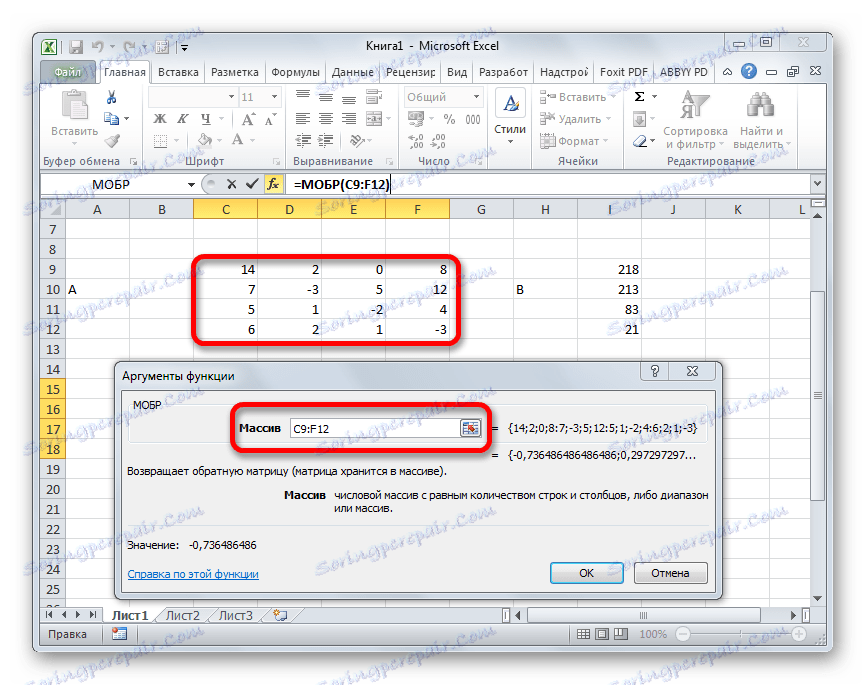
3. بادئ ذي بدء ، للعثور على جذور المعادلة ، نحتاج إلى إيجاد المصفوفة العكسيّة للمادة الحالية. لحسن الحظ ، يحتوي Excel على مشغل خاص تم تصميمه لحل هذه المشكلة. يطلق عليه ICBM . لديها بنية بسيطة إلى حد ما:

   =МОБР(массив)

   وسيطة "Array" هي في الواقع عنوان الجدول المصدر.

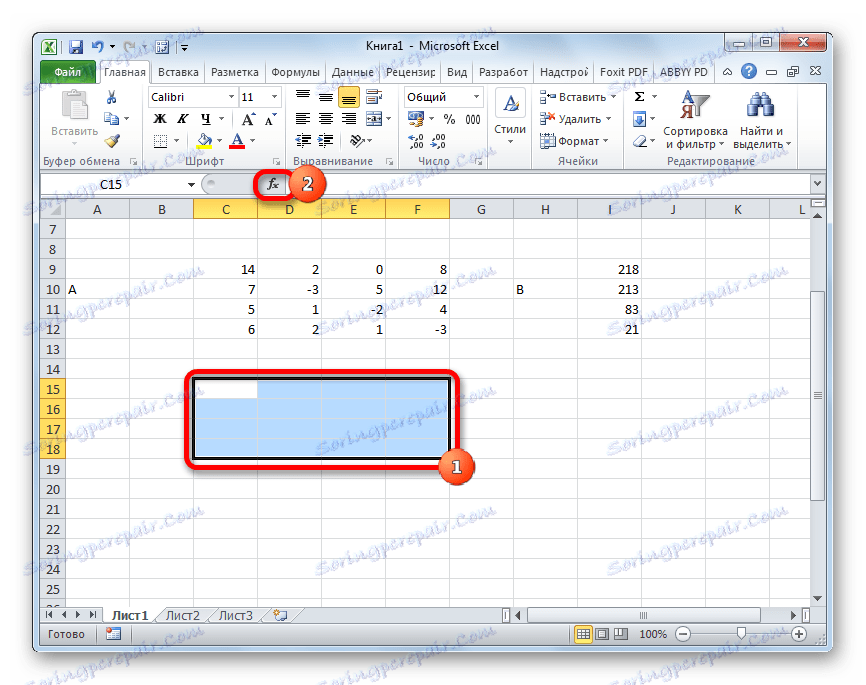
   لذا ، دعونا نختار منطقة من الخلايا الفارغة على الورقة ، وهي متساوية في الحجم مع نطاق المصفوفة الأصلية. نضغط على الزر "Insert function" (وظيفة الإدراج) ، بالقرب من خط الصيغة.

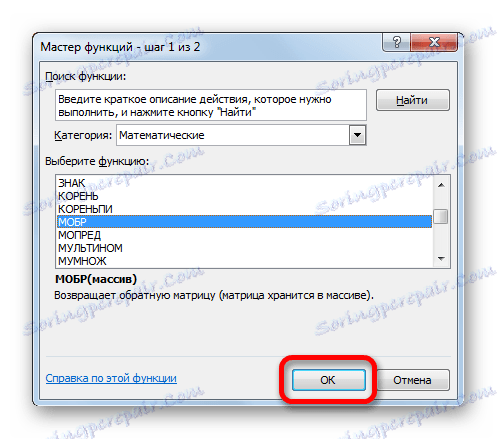
4. يبدأ معالج الدالة . لنذهب إلى فئة "رياضيات" . في القائمة المعروضة نحن نبحث عن اسم "MOBR" . بعد العثور عليه ، حدده وانقر على زر "موافق" .
5. يتم تشغيل نافذة الوسيطة الخاصة بوظيفة MOBR. أنه يحتوي على حقل واحد فقط في عدد من الحجج - "صفيف" . هنا تحتاج إلى تحديد عنوان جدول أعمالنا. لهذا الغرض ، قمنا بتعيين المؤشر في هذا الحقل. ثم ، اضغط باستمرار على زر الماوس الأيسر وحدد المنطقة على الورقة حيث توجد المصفوفة. كما ترى ، يتم إدخال البيانات المتعلقة بإحداثيات الموقع تلقائيًا في حقل النافذة. بعد الانتهاء من هذه المهمة ، سيكون أكثرها وضوحا هو الضغط على زر "موافق" ، ولكن لا تسرع. الحقيقة هي أن النقر على هذا الزر يعادل استخدام الأمر Enter . ولكن عند العمل مع المصفوفات بعد إكمال إدخال الصيغة ، يجب عدم النقر فوق الزر Enter ، ولكن قم بعمل مجموعة من اختصارات لوحة المفاتيح Ctrl + Shift + Enter . نقوم بتنفيذ هذه العملية.
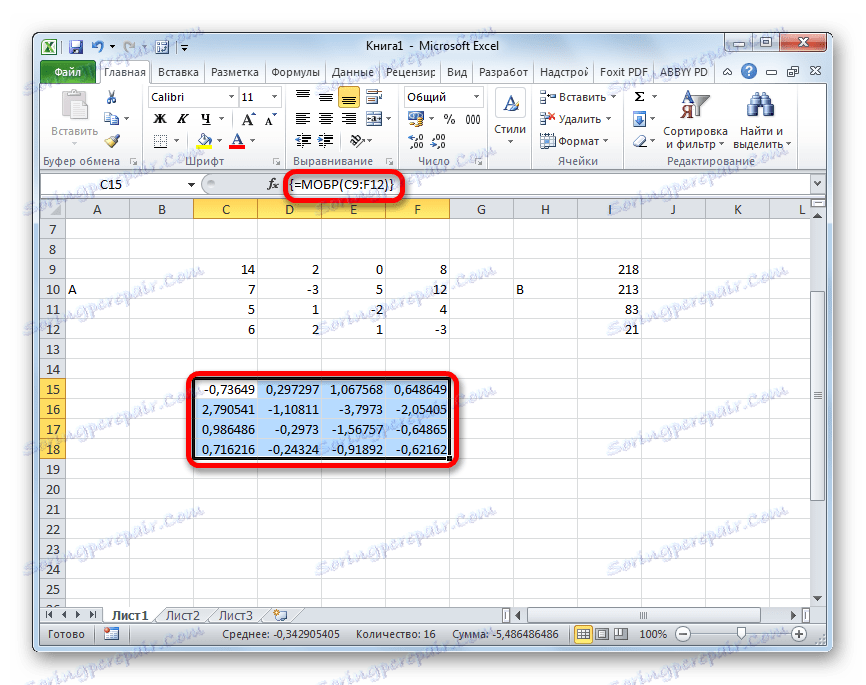
6. لذا ، بعد ذلك ، يقوم البرنامج بإجراء عمليات حسابية وعلى المخرجات في المنطقة المخصصة سابقًا لدينا معكوس مصفوفة لهذا.
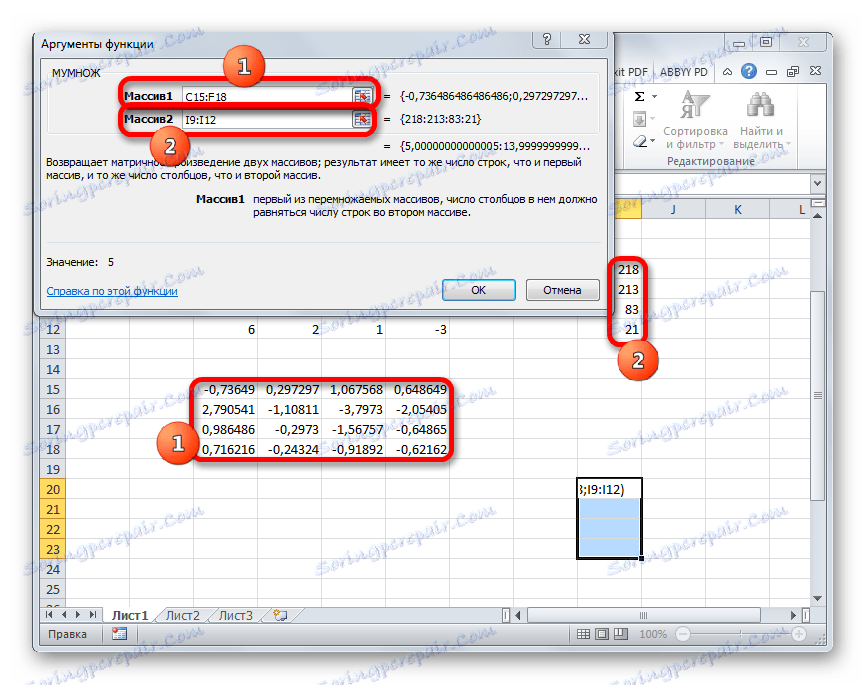
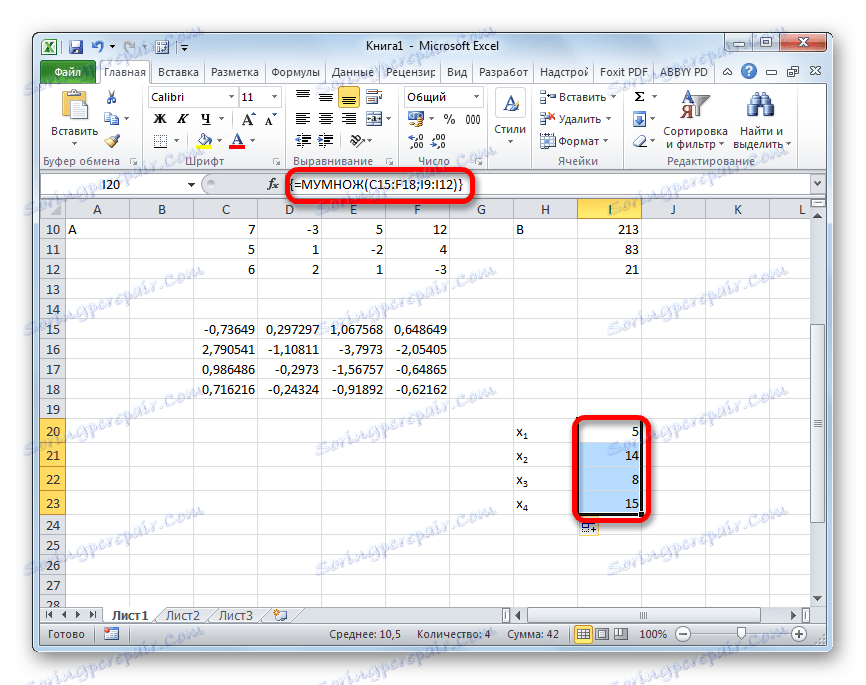
7. والآن نحتاج إلى ضرب المصفوفة العكسيّة بالمصفوفة B ، التي تتكون من عمود واحد من القيم الواقعة بعد علامة المساواة في التعبيرات. لضرب الجداول في Excel هناك أيضا وظيفة منفصلة ، والتي تسمى HUMAN . يحتوي هذا البيان على بناء الجملة التالي:

   =МУМНОЖ(Массив1;Массив2)

   نختار النطاق ، في حالتنا تتكون من أربع خلايا. ثم أعد تشغيل " معالج الدالة" مرة أخرى بالنقر فوق الرمز "إدراج دالة" .

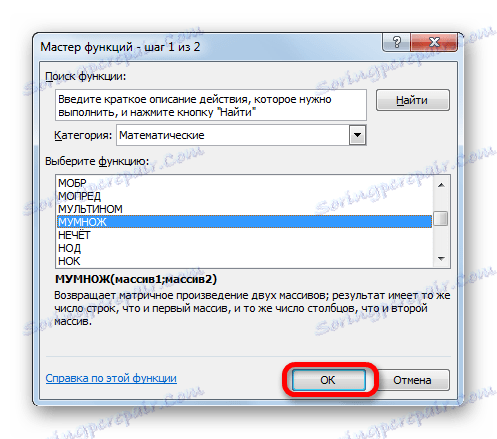
8. في الفئة "رياضيات" ، معالج بدء الوظائف ، حدد اسم "HUMBLE" وانقر على زر "OK" .
9. نافذة الحجج الدالة MULTI . في الحقل "Array1" ندخل إحداثيات لدينا المصفوفة معكوس. لهذا ، كما في المرة الأخيرة ، قمنا بتعيين المؤشر في الحقل ومع الضغط على زر الماوس الأيسر ، حدد الجدول المقابل مع المؤشر. نقوم بإجراء مماثل لإدخال الإحداثيات في الحقل "Array2" ، فقط هذه المرة نقوم بتحديد قيم العمود B. بعد تنفيذ الإجراءات المذكورة أعلاه ، لا تتعجل مرة أخرى للضغط على الزر "موافق" أو مفتاح Enter ، واكتب Ctrl + Shift + Enter .
10. بعد هذا الإجراء ، يتم عرض جذور المعادلة في الخلية المحددة مسبقًا: X1 و X2 و X3 و X4 . سيتم ترتيبها بالتسلسل. وبالتالي ، يمكننا القول إننا حلنا هذا النظام. من أجل التحقق من صحة الحل ، يكفي استبدال هذه الجذور بالنظام الأصلي للتعبيرات. إذا تمت ملاحظة المساواة ، فإن هذا يعني أن نظام المعادلات المقدمة قد تم حله بشكل صحيح.

الدرس: المصفوفة العكسية في Excel

الطريقة 2: تحديد المعلمات

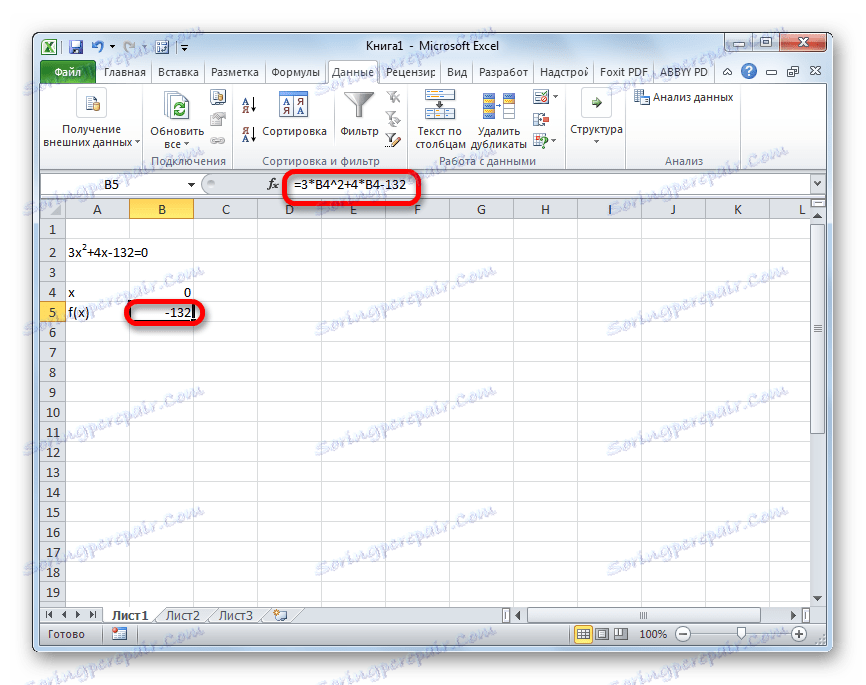
الطريقة الثانية المعروفة لحل نظام المعادلات في Excel هي تطبيق طريقة اختيار المعلمات. يكمن جوهر هذه الطريقة في البحث عن العكس. بمعنى ، بناءً على النتيجة المعروفة ، نبحث عن حجة غير معروفة. دعونا نستخدم المعادلة التربيعية

3x^2+4x-132=0

1. افترض قيمة x لـ تساوي 0 . نقوم بحساب القيمة المقابلة f (x) عن طريق تطبيق الصيغة التالية:

   =3*x^2+4*x-132

   بدلاً من قيمة "X" ، قم باستبدال عنوان الخلية حيث يوجد الرقم 0 ، الذي أخذناه لـ x ، .

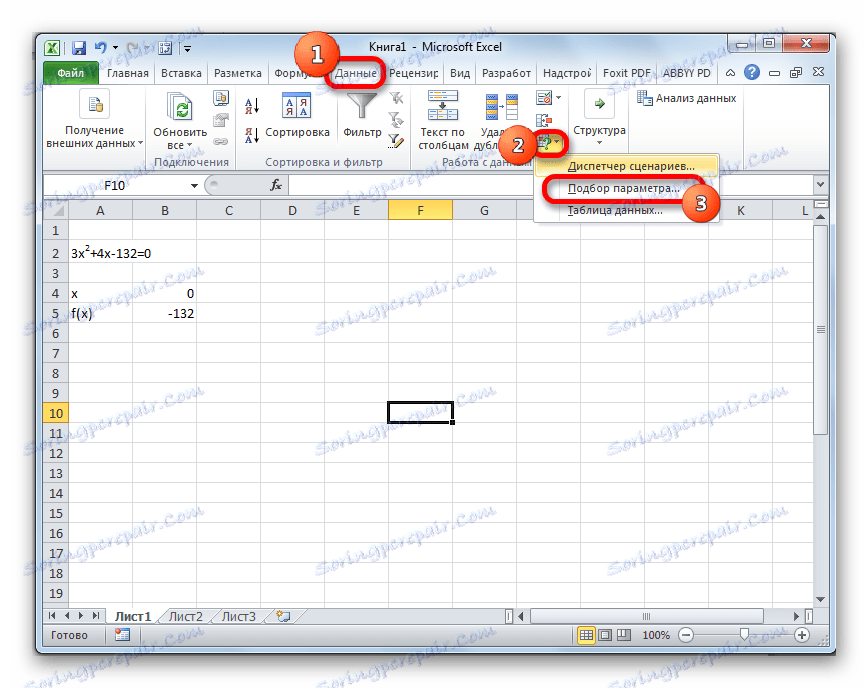
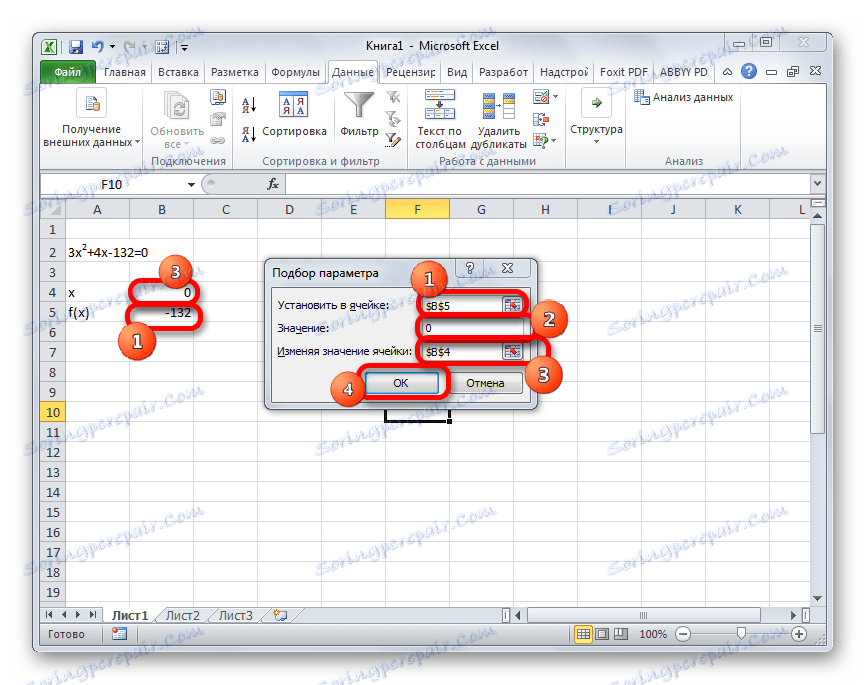
2. انتقل إلى علامة التبويب "البيانات" . انقر على زر "تحليل ماذا لو" . يقع هذا الزر على الشريط في مربع الأداة "العمل مع البيانات" . يتم عرض قائمة منسدلة. حدد العنصر "تحديد المعلمة ..." فيه .
3. يبدأ الإطار لاختيار المعلمة. كما ترون ، فإنه يتكون من ثلاثة حقول. في الحقل "Set in the cell" ، نحدد عنوان الخلية التي توجد بها الصيغة f (x) ، التي تم حسابها من قبلنا قبل قليل بقليل. في حقل "القيمة" ، أدخل الرقم "0" . في الحقل "تغيير القيم" ، نحدد عنوان الخلية التي توجد فيها قيمة x ، التي سبق أن افترضنا أنها تساوي 0 . بعد الانتهاء من هذه الخطوات ، انقر فوق الزر "موافق" .
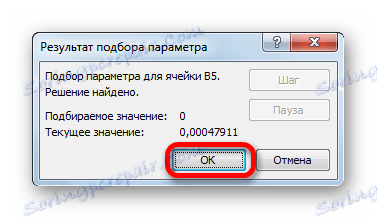
4. بعد ذلك ، سيقوم Excel بإجراء الحساب عن طريق تحديد المعلمة. سيتم الإبلاغ عن ذلك من خلال نافذة المعلومات التي ظهرت. في ذلك ، انقر على زر "موافق" .
5. ستكون نتيجة حساب جذر المعادلة في الخلية التي قمنا بتعيينها في الحقل "تغيير القيم" . في حالتنا ، كما سنرى ، x تساوي 6 .

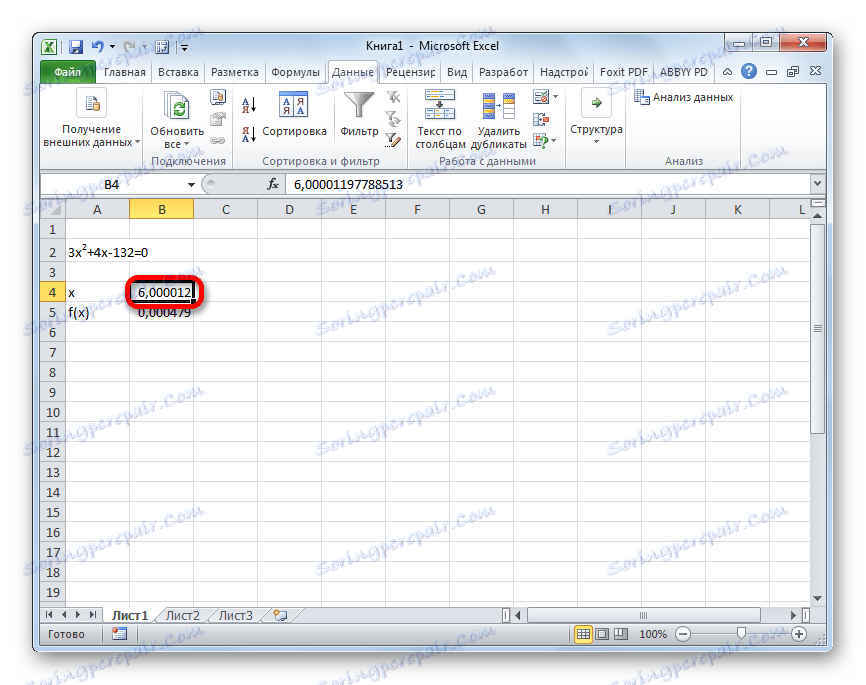
يمكن أيضًا التحقق من هذه النتيجة عن طريق استبدال هذه القيمة في التعبير المحول بدلاً من القيمة x .

الدرس: اختيار المعلمة في Excel

الطريقة الثالثة: طريقة Cramer

الآن دعونا نحاول حل نظام المعادلات بطريقة Cramer. على سبيل المثال ، خذ نفس النظام الذي تم استخدامه في Mode 1 :


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


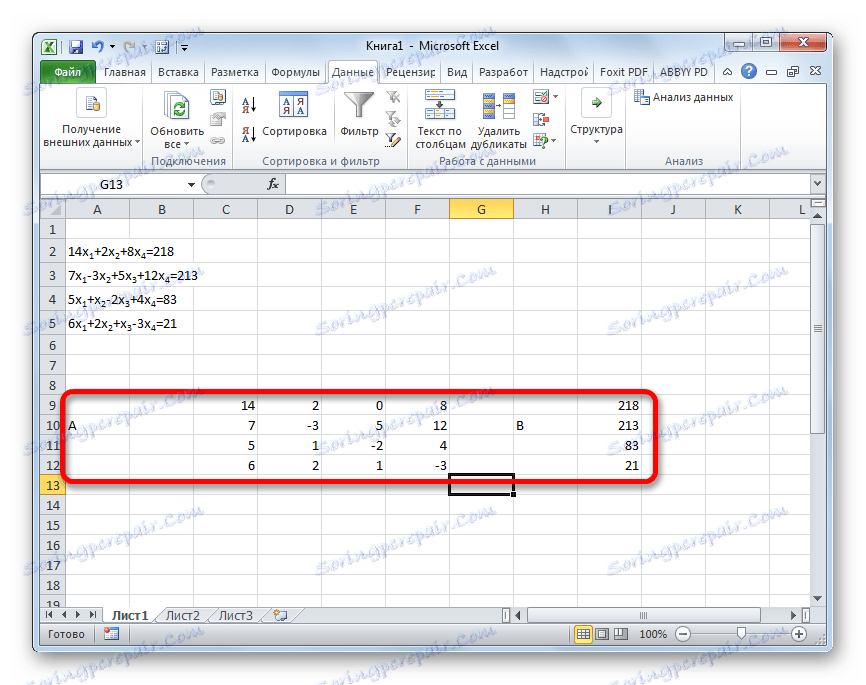
1. كما في الطريقة الأولى ، نقوم بتكوين المصفوفة أ من معاملات المعادلات والجدول ب من القيم التي تقف بعد علامة "مساواة" .
2. ثم نقوم بإنشاء أربعة جداول أخرى. كل منها نسخة من المصفوفة A ، فقط لهذه النسخ يتم استبدال عمود واحد بجدول واحد . يحتوي الجدول الأول على العمود الأول ، ويحتوي الجدول الثاني على العمود الثاني وهكذا.
3. الآن نحن بحاجة إلى حساب المحددات لجميع هذه الجداول. لن يكون لنظام المعادلات حلولًا إلا إذا كانت جميع المحددات لها قيمة مختلفة عن الصفر. لحساب هذه القيمة في Excel مرة أخرى هناك وظيفة منفصلة - MOPRED . بناء جملة هذا المشغل هو:

   =МОПРЕД(массив)

   وهكذا ، وكما هو الحال في وظيفة MBD ، فإن الوسيطة الوحيدة هي مرجع للجدول الجاري معالجته.

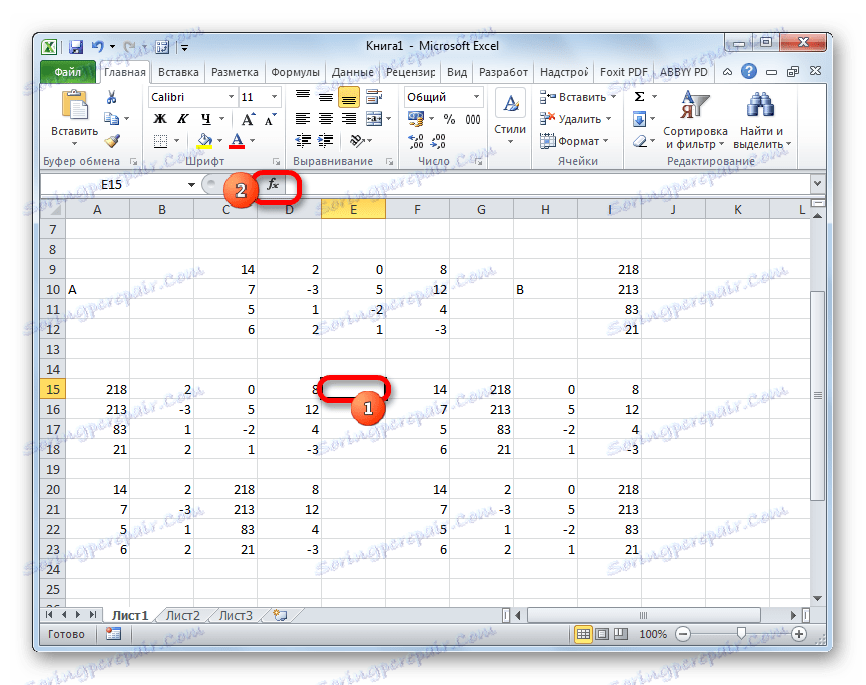
   لذلك ، حدد الخلية التي سيتم عرض محدد من المصفوفة الأولى. ثم انقر فوق الزر "إدراج وظيفة" ، وهو مألوف من الطرق السابقة.

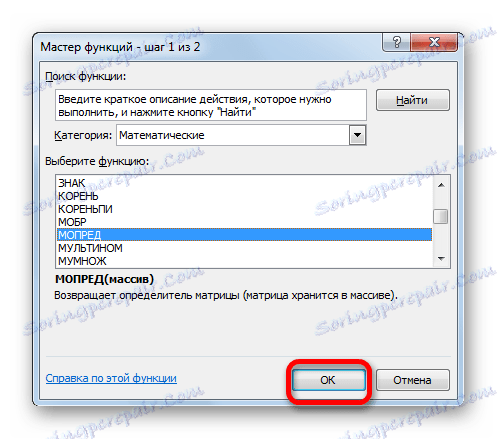
4. يتم تنشيط نافذة المعالجات . ننتقل إلى الفئة "رياضيات" ومن بين قائمة المشغلين ، نختار اسم "MOPRED" هناك . بعد ذلك ، انقر على زر "موافق" .
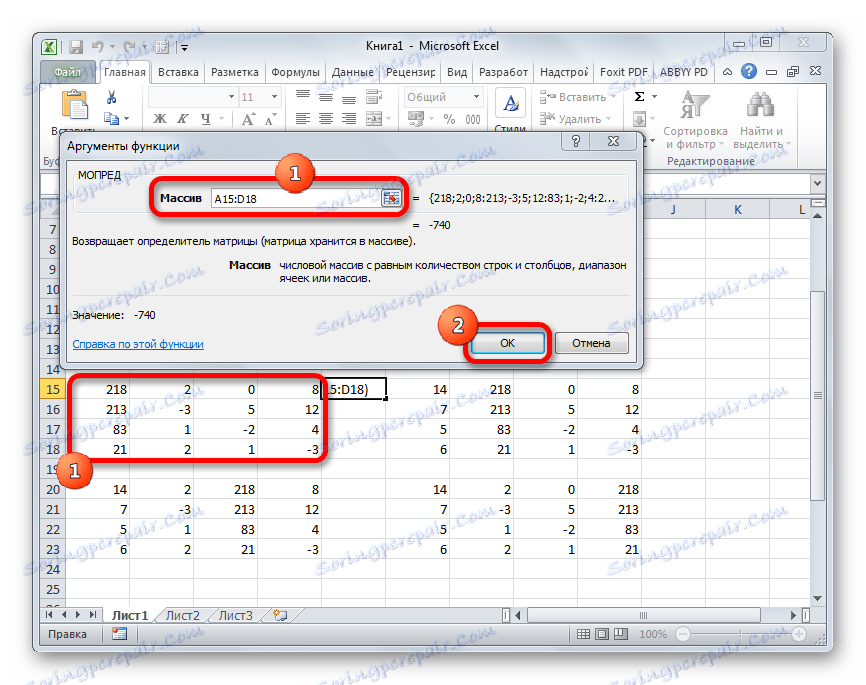
5. يتم تشغيل نافذة الحجج الخاصة بوظيفة MOPED . كما ترون ، فإنه يحتوي على حقل واحد فقط - "صفيف" . في هذا المجال ، أدخلنا عنوان أول مصفوفة تم تحويلها. للقيام بذلك ، قم بتعيين المؤشر في الحقل ، ثم حدد نطاق المصفوفة. بعد ذلك ، انقر على زر "موافق" . هذه الدالة تخرج النتيجة في خلية واحدة ، وليس صفيف ، لذلك لا تحتاج إلى الضغط على Ctrl + Shift + Enter للحصول على الحساب.
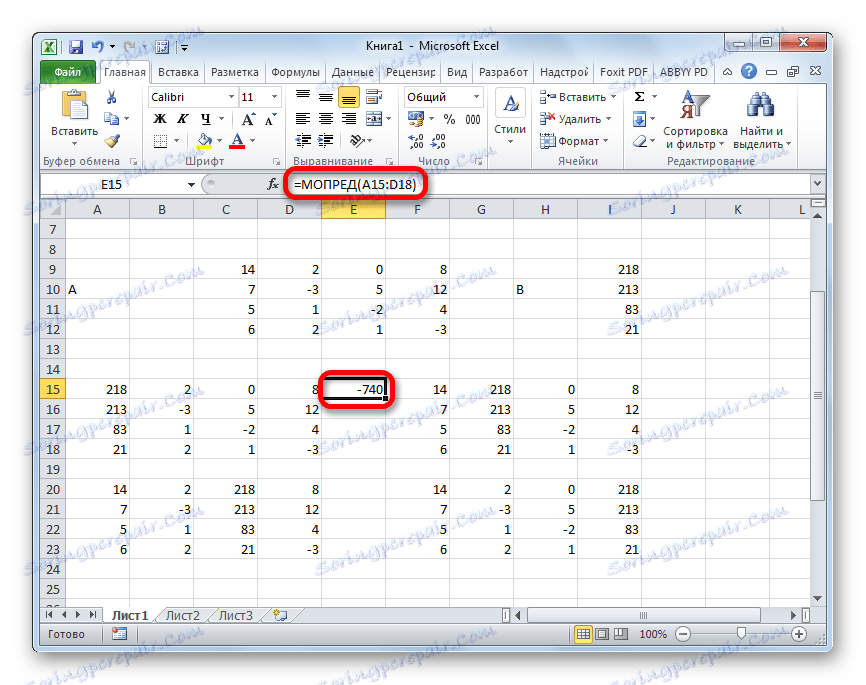
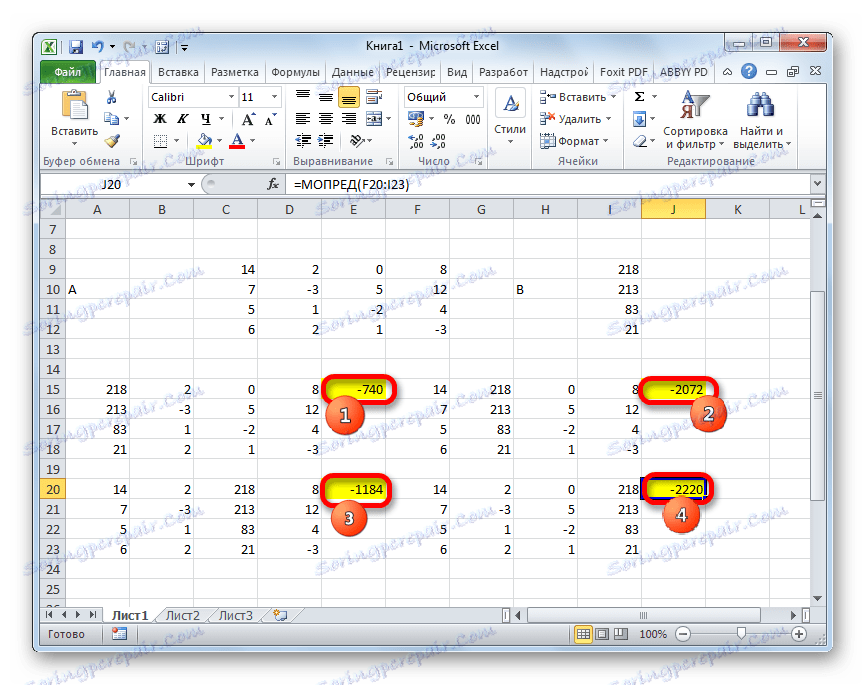
6. تقوم الدالة بحساب النتيجة وإخراجها إلى خلية محددة مسبقًا. كما ترون ، في حالتنا المحدد هو -740 ، أي أنه لا يساوي الصفر ، وهو مناسب لنا.
7. وبالمثل ، نحسب محددات الجداول الثلاثة المتبقية.
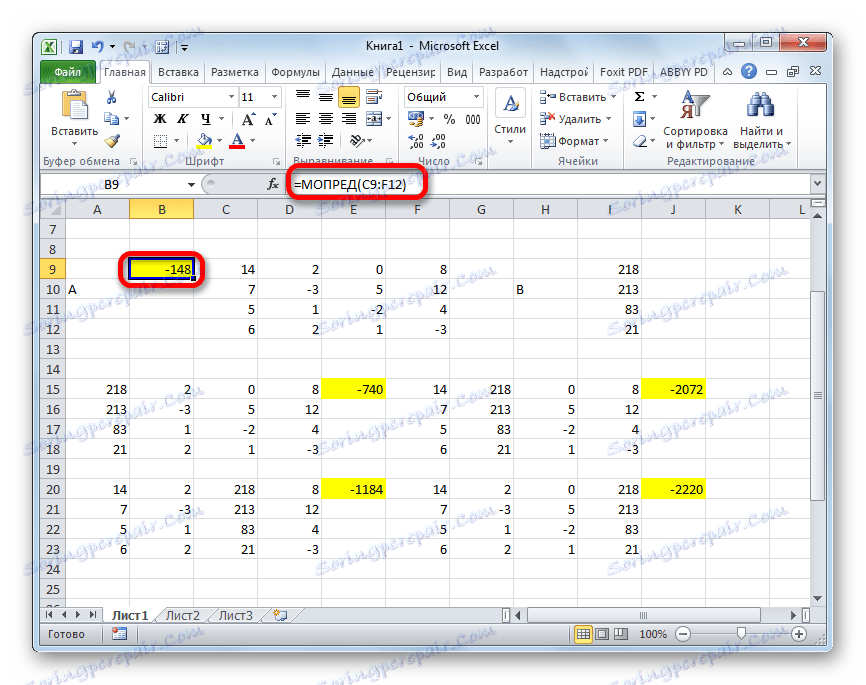
8. في المرحلة النهائية ، نحسب عامل محدد للمصفوفة الأساسية. الإجراء هو نفسه لكل الخوارزمية. كما ترى ، فإن المحدد الأساسي للجدول الأساسي يختلف أيضًا عن الصفر ، وبالتالي تعتبر المصفوفة غير متجانسة ، أي أن نظام المعادلات يحتوي على حلول.
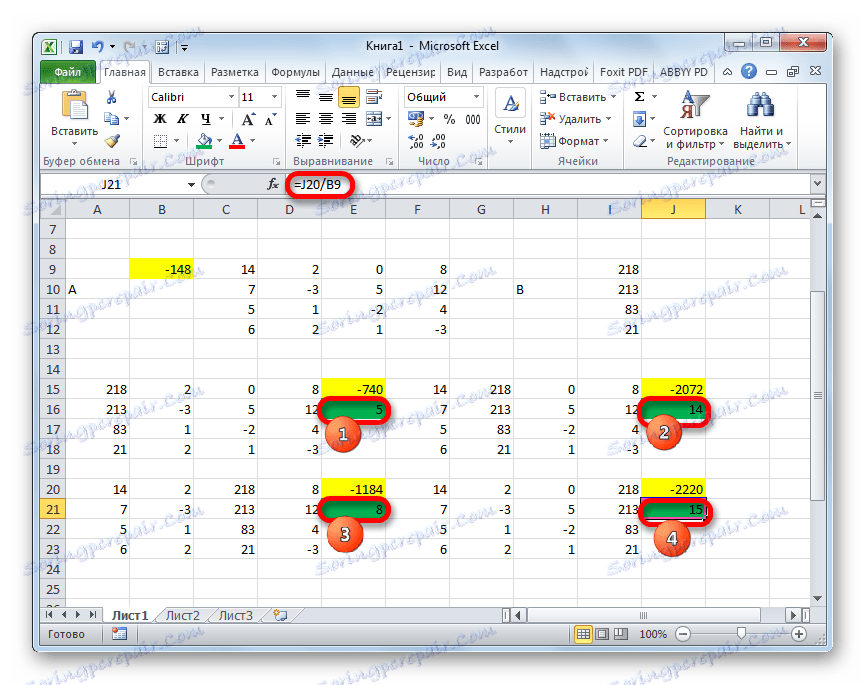
9. الآن حان الوقت للعثور على جذور المعادلة. سيكون جذر المعادلة مساوياً لنسبة المحدد في المصفوفة المحولة المقابلة إلى محدد الجدول الأساسي. وهكذا ، بعد تقسيم جميع المحددات الأربعة للمصفوفات المحولة واحدا تلو الآخر -148 ، والذي هو المحدد للجدول الأصلي ، نحصل على أربعة جذور. كما ترون ، فهي تساوي قيم 5 و 14 و 8 و 15 . وبالتالي ، فإنها تتطابق تمامًا مع الجذور التي وجدناها باستخدام المصفوفة العكسيّة في الطريقة الأولى ، التي تؤكد صحة حل نظام المعادلات.

الطريقة الرابعة: أسلوب Gauss

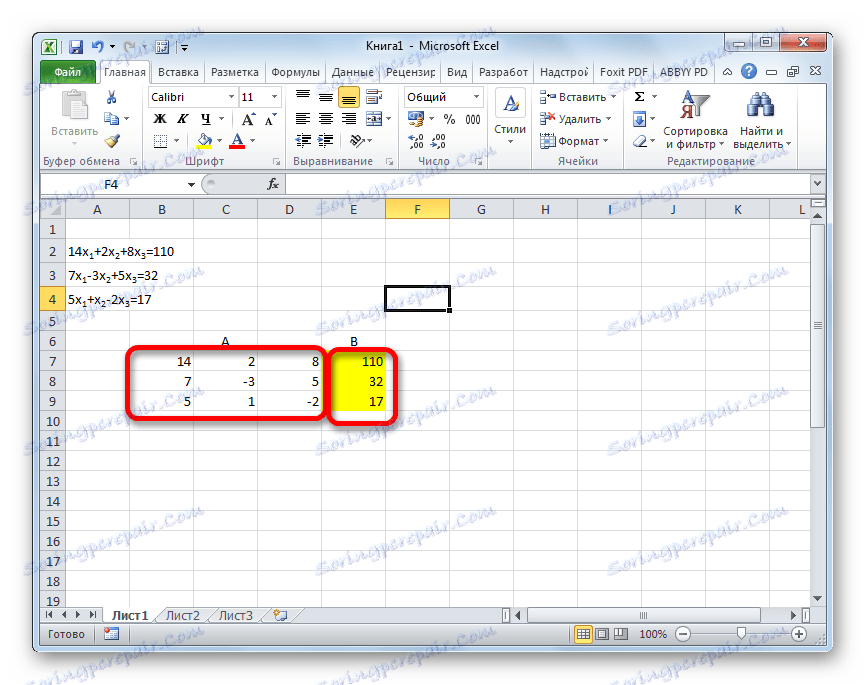
يمكن أيضًا حل نظام المعادلات باستخدام طريقة Gauss. على سبيل المثال ، لنأخذ نظامًا أبسطًا من معادلات ثلاثة مجهولة:


14 x1 +2 x2 +8 x3 =110
7 x1 -3 x2 +5 x3 =32
5 x1 + x2 -2 x3 =17


1. مرة أخرى ، نسجِّل المعاملات على التوالي في الجدول ( أ) ، والشروط الحرة الموجودة بعد علامة "يساوي" في الجدول ب. ولكن هذه المرة سنجعل كلا التقربتين أقرب ، لأن ذلك سيكون ضروريًا لنا للعمل في المستقبل. الشرط المهم هو أن القيمة في الخلية الأولى من المصفوفة A تختلف عن الصفر. في الحالة المعاكسة ، يجب إعادة ترتيب الصفوف في الأماكن.
2. انسخ الصف الأول من مصفوفتين متصلين في صف أدناه (للتوضيح ، يمكنك تخطي سطر واحد). في الخلية الأولى ، التي تقع في الصف أقل من السابقة ، أدخلنا الصيغة التالية:

   =B8:E8-$B$7:$E$7*(B8/$B$7)

   إذا قمت بترتيب المصفوفات بشكل مختلف ، فسيكون لعناوين خلايا الصيغة قيمة مختلفة بالنسبة لك ، ولكن يمكنك حسابها بمقارنتها مع الصيغ والصور التي يتم تقديمها هنا.

   بعد إدخال الصيغة ، حدد صف الخلايا بأكمله واضغط Ctrl + Shift + Enter . سيتم تطبيق صيغة الصفيف على الصف وسيتم ملؤه بالقيم. وهكذا نحن طرح من السطر الثاني الأول ، مضروبة في نسبة المعاملات الأولى من أول تعبيرين من النظام.

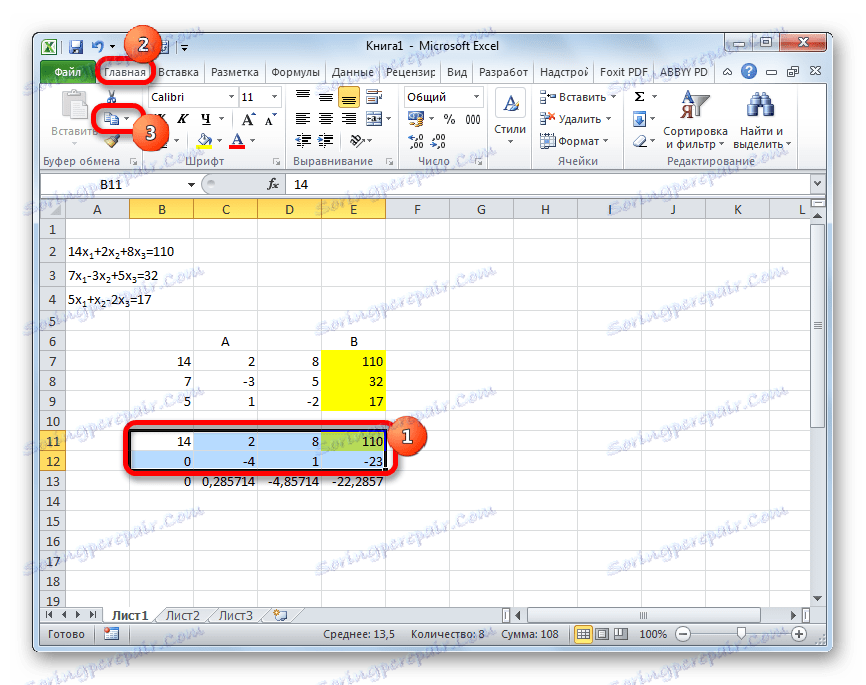
3. بعد ذلك ، انسخ السطر الناتج والصقه في السطر أدناه.
4. حدد أول سطرين بعد السطر المفقود. انقر فوق الزر "نسخ" الموجود على الشريط في علامة التبويب "Home" .
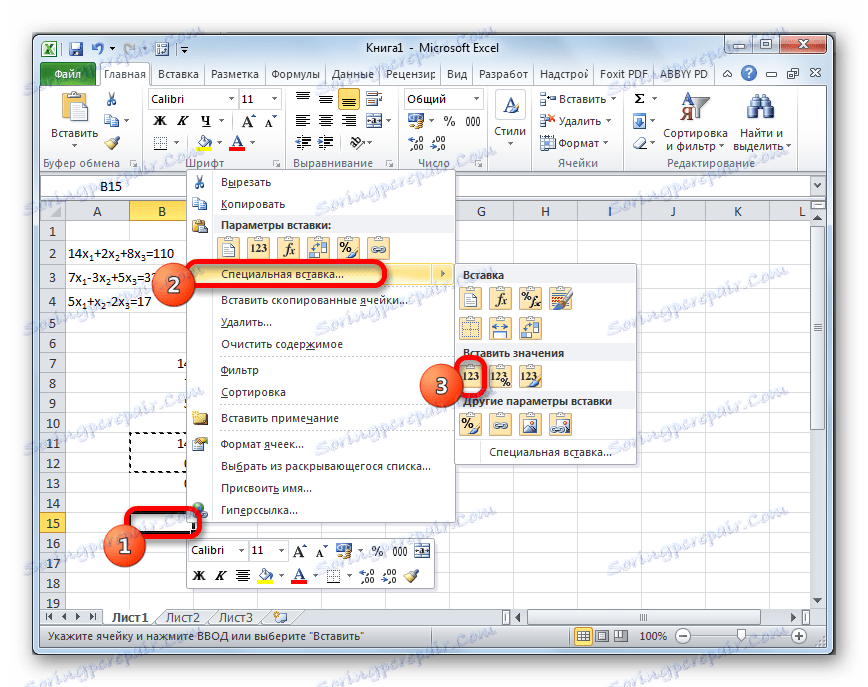
5. نتخطى السطر بعد آخر سجل في الورقة. حدد الخلية الأولى في السطر التالي. انقر بالزر الأيمن للفأرة. في قائمة السياقات المفتوحة ، نقوم بتمرير المؤشر فوق العنصر "لصق خاص" . في القائمة الإضافية التي تبدأ ، حدد عنصر "القيم" .
6. في السطر التالي ، أدخل صيغة الصفيف. تقوم بطرح الصف الثاني من الصف الثالث لمجموعة البيانات السابقة ، مضروبة في نسبة المعامل الثاني للصفين الثالث والثاني. في حالتنا ، سيكون للصيغة النموذج التالي:

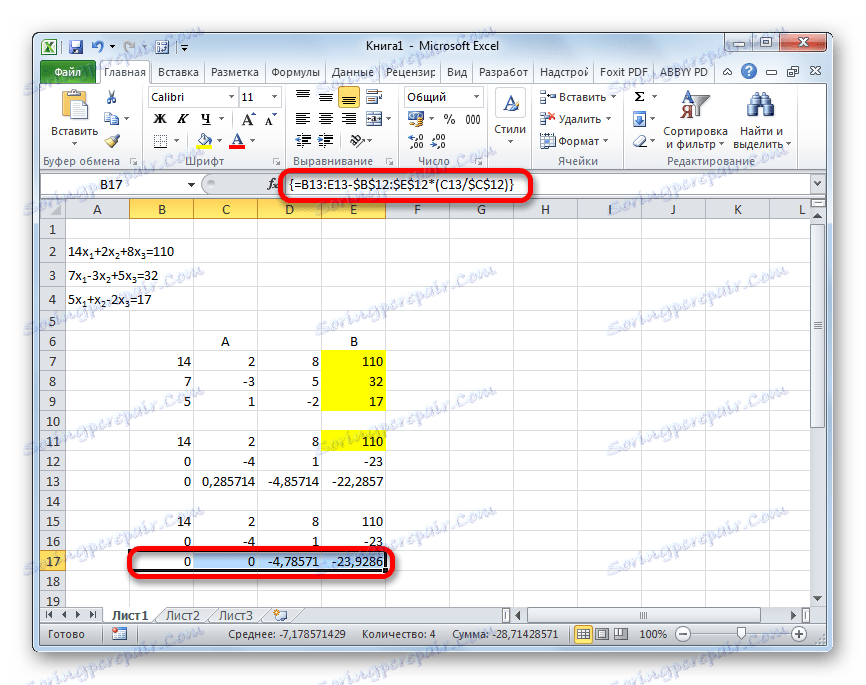
   =B13:E13-$B$12:$E$12*(C13/$C$12)

   بعد إدخال الصيغة ، حدد السلسلة بأكملها وقم بتطبيق اختصار لوحة المفاتيح Ctrl + Shift + Enter .

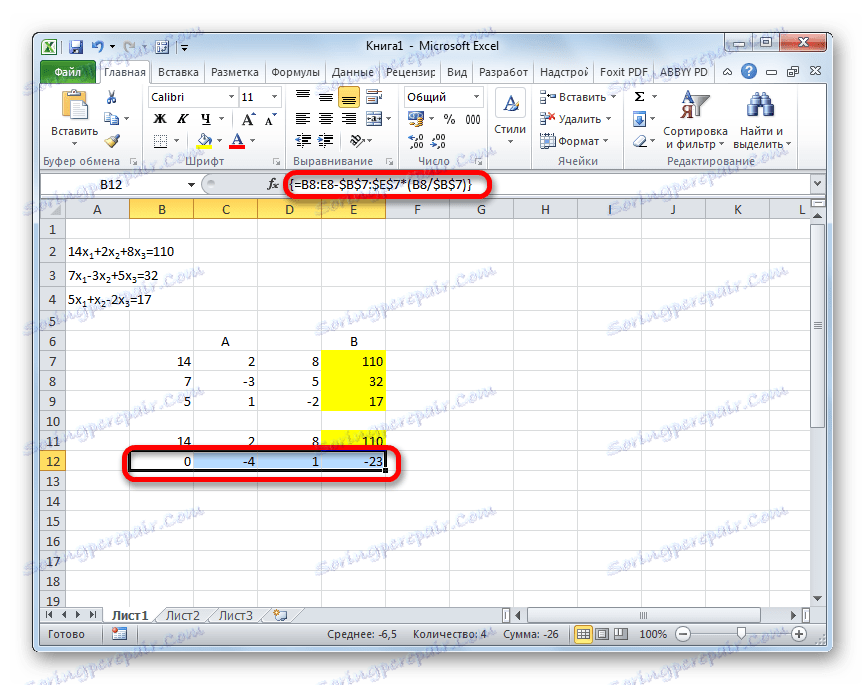
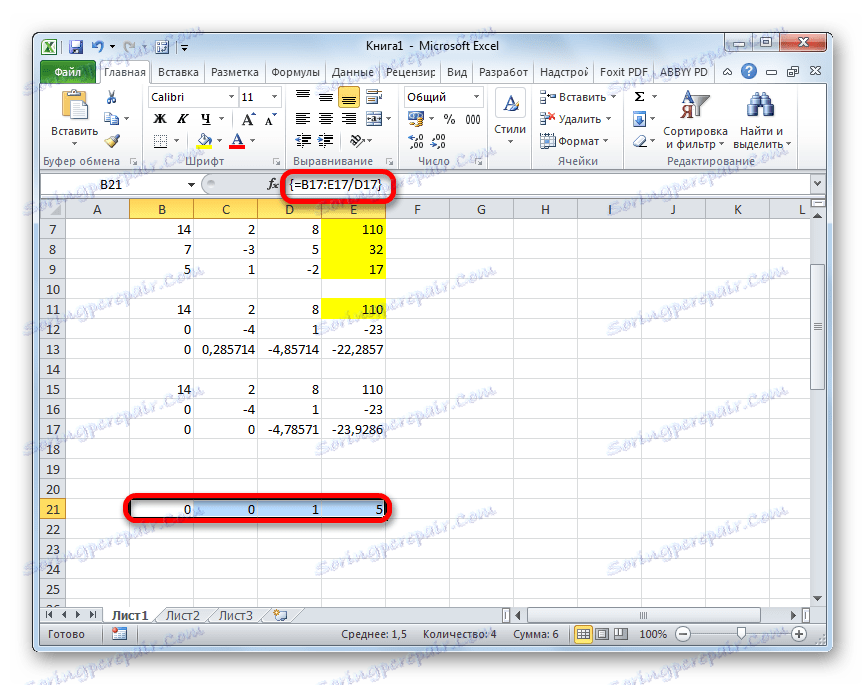
7. الآن من الضروري إجراء تشغيل عكسي باستخدام أسلوب Gauss. نحن نتخطى ثلاثة سطور من السجل الأخير. في السطر الرابع ، ندخل صيغة المصفوفة:

   =B17:E17/D17

   وهكذا ، نقسم السطر الأخير الذي حسبناه بمعامله الثالث. بعد كتابة الصيغة ، حدد السطر بالكامل واضغط Ctrl + Shift + Enter .

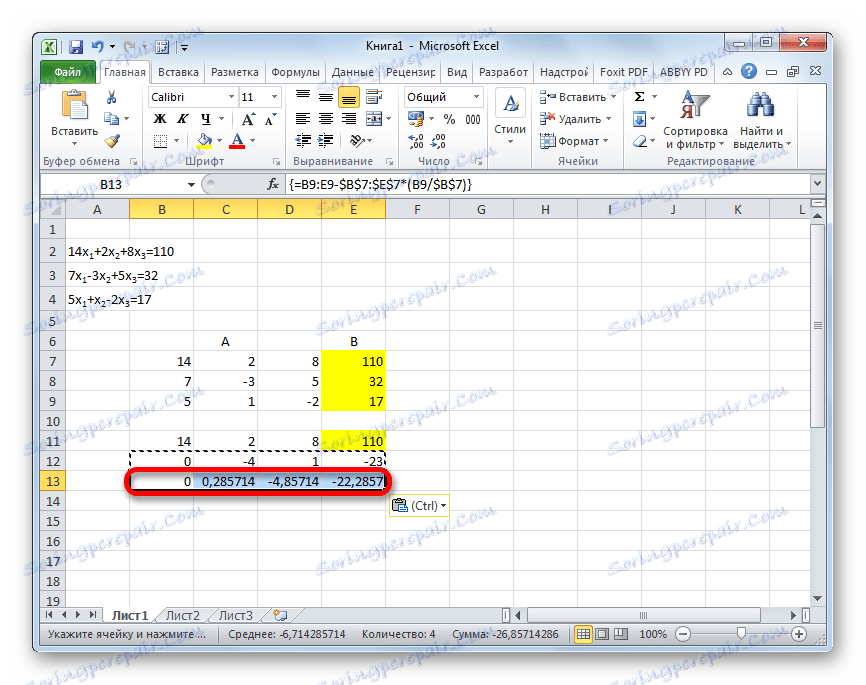
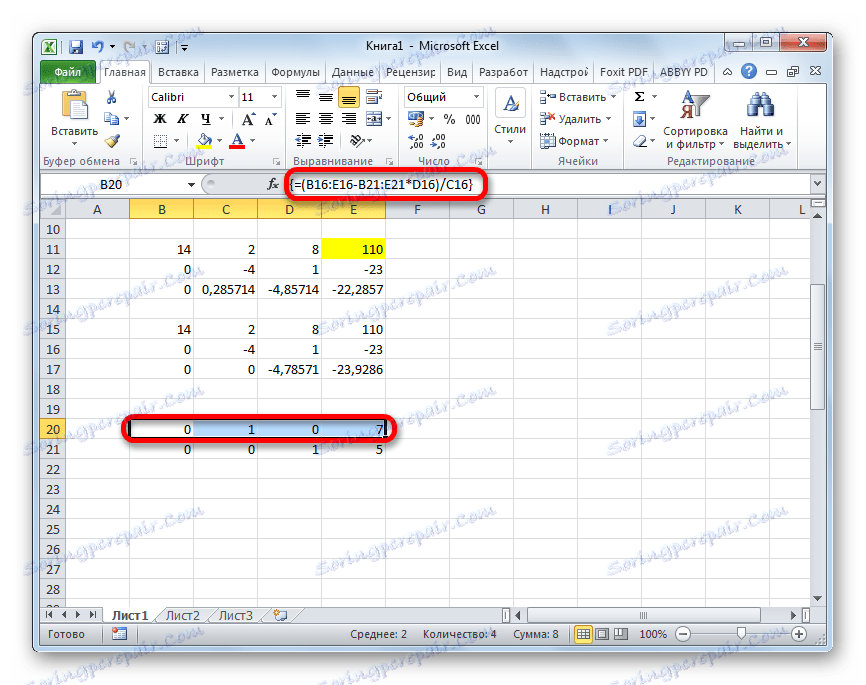
8. نرتفع على خط لأعلى وندخل فيه الصيغة التالية للمصفوفة:

   =(B16:E16-B21:E21*D16)/C16

   نضغط على المجموعة المعتادة من المفاتيح لتطبيق صيغة الصفيف.

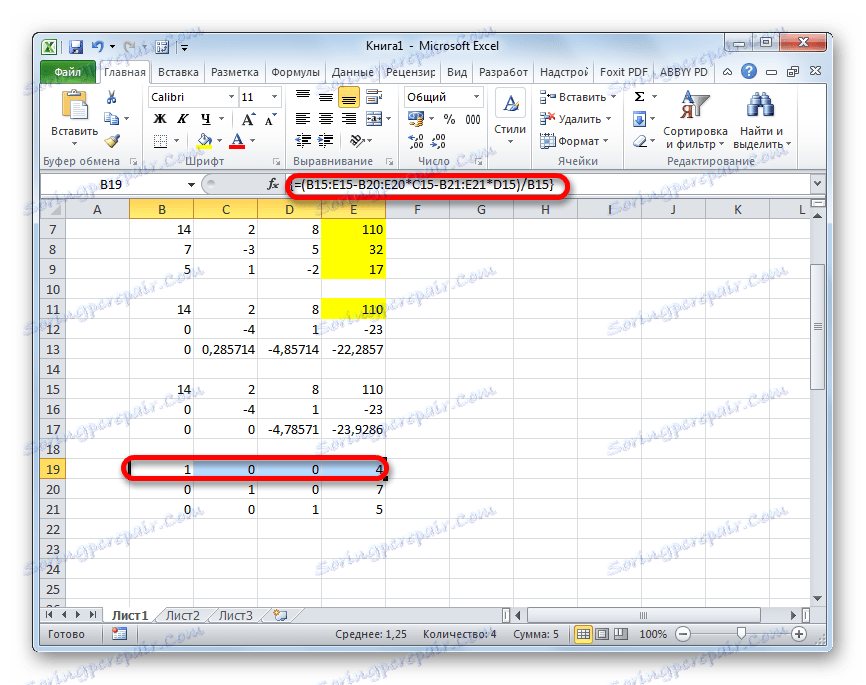
9. نرتفع بخطًا أعلى. في ذلك ندخل صيغة صفيف النموذج التالي:

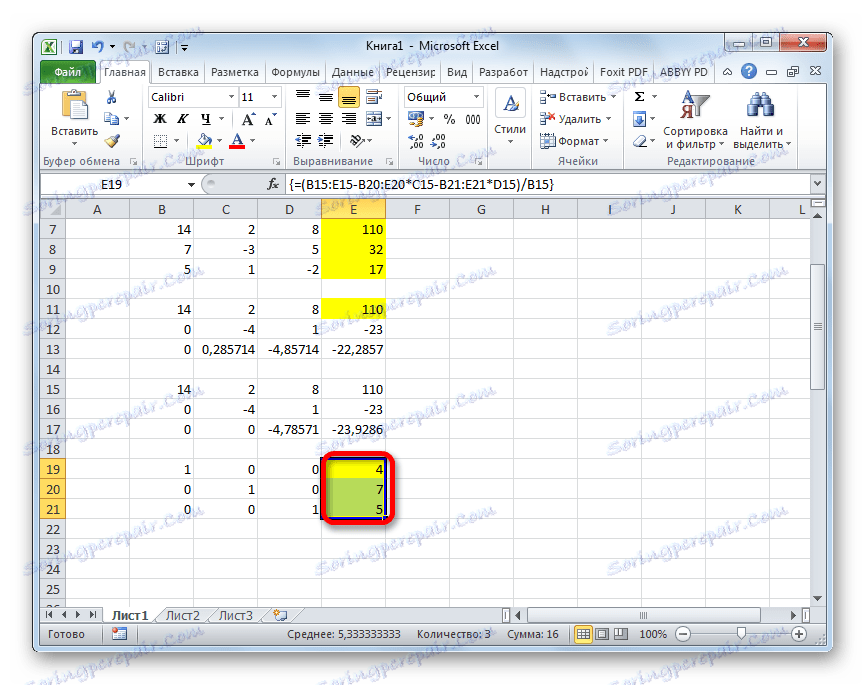
   =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

   مرة أخرى ، حدد السطر بالكامل وقم بتثبيت تركيبة المفاتيح Ctrl + Shift + Enter .

10. انظر الآن إلى الأرقام التي تم الحصول عليها في العمود الأخير من كتلة الأسطر الأخيرة ، والتي تم حسابها من قبلنا سابقًا. هذه الأرقام ( 4 و 7 و 5 ) هي جذور النظام المعطى من المعادلات. يمكنك التحقق من ذلك عن طريق استبدالها بدلاً من X1 و X2 و X3 في التعبيرات.

كما ترى ، في نظام Excel يمكن حل نظام المعادلات بواسطة عدد من الأساليب ، لكل منها مميزاته وعيوبه. ولكن يمكن تقسيم جميع هذه الطرق بشكل مشروط إلى مجموعتين كبيرتين: المصفوفة واستخدام الأداة لاختيار المعلمات. في بعض الحالات ، لا تكون طرق المصفوفة دائمًا مناسبة لحل المشكلة. على وجه الخصوص ، عندما يكون محدد المصفوفة هو صفر. في حالات أخرى ، يكون للمستخدم حرية تحديد الخيار الذي يعتبره أكثر ملاءمة لنفسه.

• ← بناء القطع المكافئ في Microsoft Excel
• خلق زر في مايكروسوفت اكسل →